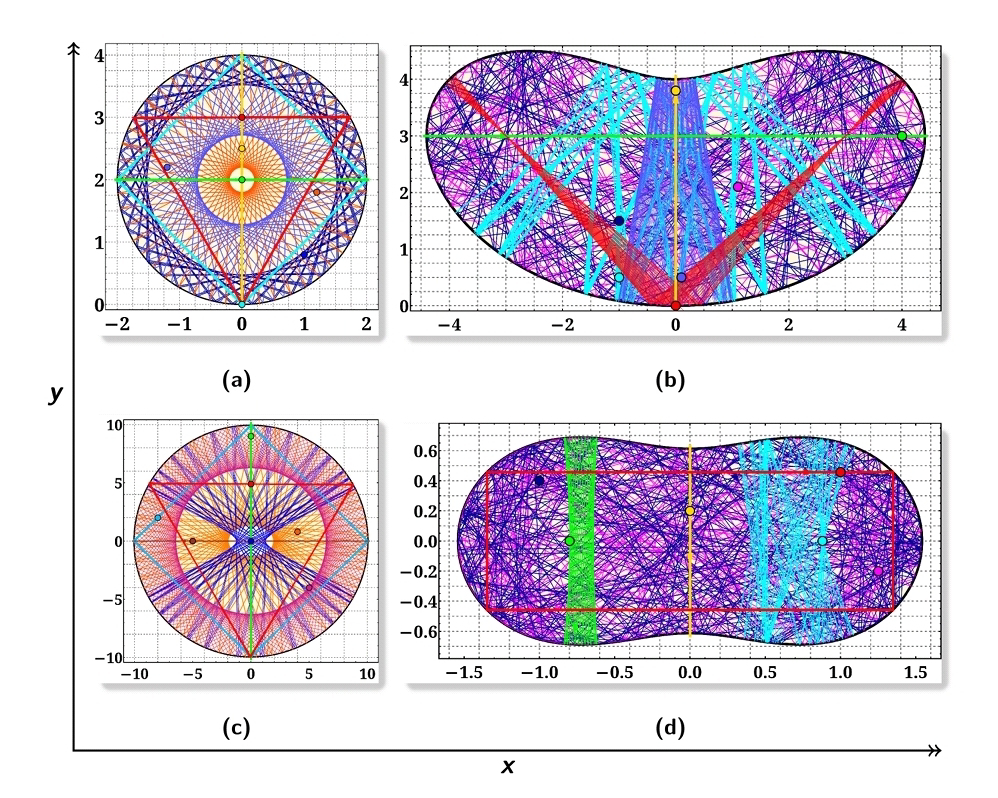
<< ️In this paper, (AA) introduced and extensively investigated dynamical billiards on the surface of a cone with a tilted base. Upon varying the cone angle β, corresponding to a deficit angle
2πχ = 2π(1 − sin(β)), and tilt angle γ, (They) identified three distinct types of trajectories with associated Poincaré map for conical billiards: rim, hourglass, and mixed. >>
<< ️Region I, where Poincaré space consists of rim, hourglass, and mixed trajectories; Region IIB, where Poincaré space consists of only hourglass and mixed trajectories; and Region IIA, in which (They) find choices of γ and χ for which almost all trajectories are strongly mixing. (..) (AA) also developed a scheme for identifying strongly mixing trajectories. >>
<< ️Furthermore, (They) were able to show that a dynamical billiard on a surface with exclusively convex and positive Gaussian curvature in three dimensions can still exhibit ergodic behavior in certain parameter regimes. >>
<< ️A particularly intriguing feature of this system is that by tuning χ and γ, nearly all points in (θ,ϕ) Poincaré space describing conical line segments in between bounces can be placed at the edge between chaotic and integrable dynamics. Thus this work highlights the potential of conical billiards as a model system for exploring intriguing problems inspired by neural networks at the “edge of chaos”. >>
Lara Braverman, David R. Nelson. Transition to chaos with conical billiards. arXiv: 2508.02786v1 [nlin.CD]. Aug 4, 2025.
Phys. Rev. E 112, 044221. Oct 21, 2025.
Also: billiard, chaos, transition, in https://www.inkgmr.net/kwrds.html
Keywords: gst, billiards, conical billiard, chaos, transitions, neural networks