# aibot: noise balance and stationary distribution of stochastic gradient descent.

<< The stochastic gradient descent (SGD) algorithm is the algorithm (is used) to train neural networks. However, it remains poorly understood how the SGD navigates the highly nonlinear and degenerate loss landscape of a neural network. >>

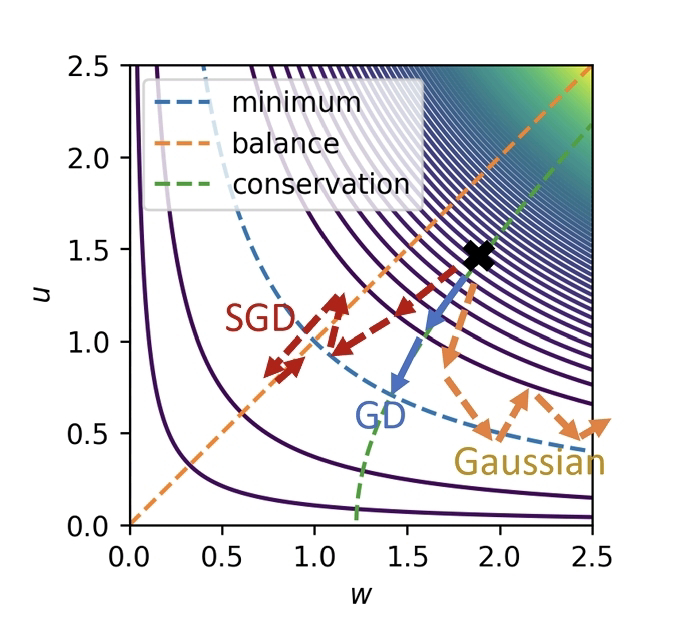
<< In this work, (AA) show that the minibatch noise of SGD regularizes the solution towards a noise-balanced solution whenever the loss function contains a rescaling parameter symmetry. Because the difference between a simple diffusion process and SGD dynamics is the most significant when symmetries are present, (AA) theory implies that the loss function symmetries constitute an essential probe of how SGD works. (They) then apply this result to derive the stationary distribution of stochastic gradient flow for a diagonal linear network with arbitrary depth and width. >>

<< The stationary distribution exhibits complicated nonlinear phenomena such as phase transitions, broken ergodicity, and fluctuation inversion. These phenomena are shown to exist uniquely in deep networks, implying a fundamental difference between deep and shallow models. >>

Liu Ziyin, Hongchao Li, Masahito Ueda. Noise balance and stationary distribution of stochastic gradient descent. Phys. Rev. E 111, 065303. Jun 6, 2025.

https://journals.aps.org/pre/abstract/10.1103/PhysRevE.111.065303

Also: ai (artificial intell) (bot), network, noise, disorder & fluctuations, in https://www.inkgmr.net/kwrds.html 

Keywords: ai, artificial intelligence, noise, stochasticity, networks, neural networks, deep learning,stochastic gradient descent (SGD), transitions, phase transitions, broken ergodicity, fluctuation inversion

# gst: apropos of absorbing targets, persistence exponents of self-interacting random walks

<< The persistence exponent, which characterizes the long-time decay of the survival probability of stochastic processes in the presence of an absorbing target, plays a key role in quantifying the dynamics of fluctuating systems. Determining this exponent for non-Markovian processes is known to be a difficult task, and exact results remain scarce despite sustained efforts. >> 

In their Letter, AA << consider the fundamental class of self-interacting random walks (SIRWs), which display long-range memory effects that result from the interaction of the random walker at time 𝑡 with the territory already visited at earlier times 𝑡′ <𝑡. (AA)  compute exactly the persistence exponent for all physically relevant SIRWs. As a byproduct, (They) also determine the splitting probability of these processes. >>

<< Besides their intrinsic theoretical interest, these results provide a quantitative characterization of the exploration process of SIRWs, which are involved in fields as diverse as foraging theory, cell biology, and nonreversible Monte Carlo methods. >>

J. Brémont, L. Régnier, et al. Persistence Exponents of Self-Interacting Random Walks. Phys. Rev. Lett. 134, 197103. May 16, 2025.

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.134.197103

arXiv:2410.18699v1 [cond-mat.stat-mech]. 

https://arxiv.org/abs/2410.18699

Also: walk, walking, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, walk, walking, self-interacting random walk, walker self-repulsion, walker self-attraction, stochasticity, absorbing targets.

# gst: accelerated first detection in discrete-time quantum walks using sharp restarts.

<< Restart is a common strategy observed in nature that accelerates first-passage processes, and has been extensively studied using classical random walks. In the quantum regime, restart in continuous-time quantum walks (CTQWs) has been shown to expedite the quantum hitting times [Phys. Rev. Lett. 130, 050802 (2023)]. >>

 Here, AA << study how restarting monitored discrete-time quantum walks (DTQWs) affects the quantum hitting times. (They) show that the restarted DTQWs outperform classical random walks in target searches, benefiting from quantum ballistic propagation, a feature shared with their continuous-time counterparts. >>

Kunal Shukla, Riddhi Chatterjee, C. M. Chandrashekar. Accelerated first detection in discrete-time quantum walks using sharp restarts. Phys. Rev. Research 7, 023069. Apr 21, 2025.

https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.7.023069

Also: walk, random, network, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, networks, randomness, walk, random walk, quantum walk, stochasticity, sharp restart.

# gst: biased random walks on networks with stochastic resetting.

<< This study explores biased random walk dynamics with stochastic resetting on general networks. (AA) show that the combination of biased random walks and stochastic resetting makes significant contributions by analyzing the search efficiency. (They) derive two analytical expressions for the stationary distribution and the mean first passage time, which are related to the spectral representation of the probability transition matrix of a biased random walk without resetting. These expressions can be used to determine the capacity of a random walker to reach the specific target and probe a finite network. >>

AA << apply the analytical results to two types of networks, pseudofractal scale-free webs and T-fractals, which are constructed through an iterative process. (They) also extend a strategy to explore other complex structure networks or larger networks by leveraging the spectral properties. >>

Anlin Li, Xiaohan Sun. Biased random walks on networks with stochastic resetting. Phys. Rev. E 111, 054309. May 16, 2025.

https://journals.aps.org/pre/abstract/10.1103/PhysRevE.111.054309

Also: walk, random, network, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, networks, randomness, random walk, stochasticity, stochastic resetting.

# gst: First-passage-time statistics of active Brownian particles: a perturbative approach.

AA << study the first-passage-time (FPT) properties of active Brownian particles to reach an absorbing wall in two dimensions. Employing a perturbation approach (They) obtain exact analytical predictions for the survival and FPT distributions for small Péclet numbers, measuring the importance of self-propulsion relative to diffusion. >>

<< While randomly oriented active agents reach the wall faster than their passive counterpart, their initial orientation plays a crucial role in the FPT statistics. Using the median as a metric, (AA) quantify this anisotropy and find that it becomes more pronounced at distances where persistent active motion starts to dominate diffusion. >>️

Yanis Baouche, Magali Le Goff, et al. First-passage-time statistics of active Brownian particles: a perturbative approach. arXiv: 2503.05401v1 [cond-mat.soft]. Mar 7, 2025.

https://arxiv.org/abs/2503.05401

Also: particle, random, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, particles, active particles, perturbation approach, randomness, stochasticity, stochastic resetting, rotational diffusion, anisotropy

# gst: stochastic Scovil-Schulz-DuBois (SSDB) machine and its three types of cycles

<< Three types of cycles are identified in the quantum jump trajectories of the Scovil–Schulz-DuBois (SSDB) machine. An R cycle as refrigeration, an H cycle as a heat engine, and an N cycle in which the machine is neutral. >>

AA << find that in the large time limit, whether the machine operates as a heat engine or refrigerator depends on the ratio between the numbers of R cycles and H cycles per unit time. Further increasing the hot bath temperature above a certain threshold does not increase the machine's power output. The cause is that, in this situation, the N cycle has a greater probability than the H cycle and R cycle. >>

<< Although the SSDB machine operates by randomly switching between these three cycles, at the level of a single quantum jump trajectory, its heat engine efficiency and the refrigerator's coefficient of performance remain constant. >>

Fei Liu, Jiayin Gu. Stochastic Scovil–Schulz-DuBois machine and its three types of cycles. Phys. Rev. E 111, 014108. Jan 3, 2025. 

https://journals.aps.org/pre/abstract/10.1103/PhysRevE.111.014108 

arXiv: 2409.04124v2 [cond-mat.stat-mech]. Jan 5, 2025. 

https://arxiv.org/abs/2409.04124

Keywords: gst, stochasticity, quantum heat engines & refrigerators, stochastic Scovil–Schulz-DuBois (SSDB) machine 

# gst: stochastic adaptation, stochastic resonance.

<< Stochastic resonance is a phenomenon possessed by some nonlinear oscillators, in which a weak signal is boosted by noise. Both the monostable and bistable Duffing oscillators can exhibit this property. However, stochastic resonance has a strong frequency-dependence, as only a band of frequencies may be boosted by noise. >>️

<< Adaptive oscillators are a subset of nonlinear oscillators that can learn the features of an external force. (In this AA work), an adaptive state is added to a Duffing oscillator. This adaptive state enables the Duffing adaptive oscillator to outperform stochastic resonance over a wide range of frequencies by learning a resonance condition. >>️

Edmon Perkins. Comparison of stochastic adaptation and stochastic resonance. Phys. Rev. E 110, 064225. Dec 27, 2024.

https://journals.aps.org/pre/abstract/10.1103/PhysRevE.110.064225 

Also: fluctuations, noise, transition, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, fluctuations, noise, transition, stochasticity, stochastic adaptation, stochastic resonance

# gst: apropos of random walks, intermittent random walks under stochastic resetting

AA << analyze a one-dimensional intermittent random walk on an unbounded domain in the presence of stochastic resetting. In this process, the walker alternates between local intensive search, diffusion, and rapid ballistic relocations in which it does not react to the target. >>

AA << demonstrate that Poissonian resetting leads to the existence of a non-equilibrium steady state. (They) calculate the distribution of the first arrival time to a target along with its mean and show the existence of an optimal reset rate. In particular, (..) the initial condition of the walker, i.e., either starting diffusely or relocating, can significantly affect the long-time properties of the search process. >>

<< the presence of distinct parameter regimes for the global optimization of the mean first arrival time when ballistic and diffusive movements are in direct competition. >>️

Rosa Flaquer-Galmes, Daniel Campos,  Vicenc Mendez. Intermittent random walks under stochastic resetting. Phys. Rev. E 109, 034103. March 4, 2024. 

https://journals.aps.org/pre/abstract/10.1103/PhysRevE.109.034103  

Also: walk, walking, random, in https://www.inkgmr.net/kwrds.html

Keywords: gst, walk, intermittent random walk, stochasticity, stochastic resetting

# gst: perform statistics of rare events in stochastic processes by defining stochastic bridges from fixed start and end points.

<< The numerical quantification of the statistics of rare events in stochastic processes is a challenging computational problem. (AA) present a sampling method that constructs an ensemble of stochastic trajectories that are constrained to have fixed start and end points (so-called stochastic bridges). (AA) then show that by carefully choosing a set of such bridges and assigning an appropriate statistical weight to each bridge, one can focus more processing power on the rare events of a target stochastic process while faithfully preserving the statistics of these rare trajectories. >>

Javier Aguilar, Joseph W. Baron, et al. 

Sampling rare trajectories using stochastic bridges. Phys. Rev. E 105, 064138. Jun 30, 2022.

https://journals.aps.org/pre/abstract/10.1103/PhysRevE.105.064138

Keywords: stochasticity, stochastic processes, stochastic bridges, large deviations, rare trajectories, rare event statistics.

# gst: small-scale random perturbations, Arnold's cat spontaneously stochastic

<< Multi-scale systems (..) may possess a fascinating property of spontaneous stochasticity: a small-scale initial uncertainty develops into a randomly chosen largescale state in a finite time, and this behavior is not sensitive to the nature and magnitude of uncertainty (..). >>

A << intriguing form is the Eulerian spontaneous stochasticity (ESS) of the velocity field itself: an infinitesimal small-scale noise triggers stochastic evolution of velocity field at finite scales and times. >>

AA << prove that a formally deterministic system with scaling symmetry yields a stochastic process with Markovian properties if it is regularized with a vanishing small-scale random perturbation. Besides its significance for understanding turbulence, (their) model extends the phenomenon of ESS beyond the scope of fluid dynamics: (AA) discuss a prototype of a feasible experiment for observing ESS in optics or electronics, as well as potential applications in other physical systems.>>

Alexei A. Mailybaev, Artem Raibekas. Spontaneously stochastic Arnold's cat. arXiv:2111.03666v1 [nlin.CD]. Nov 5,  2021.

https://arxiv.org/abs/2111.03666

keywords: gst, Arnold's cat, randomness, stochasticity, spontaneous stochasticity, small-scale random perturbations, noise, turbulence, chaos