# gst: discontinuous transition to chaos in a canonical random neural network

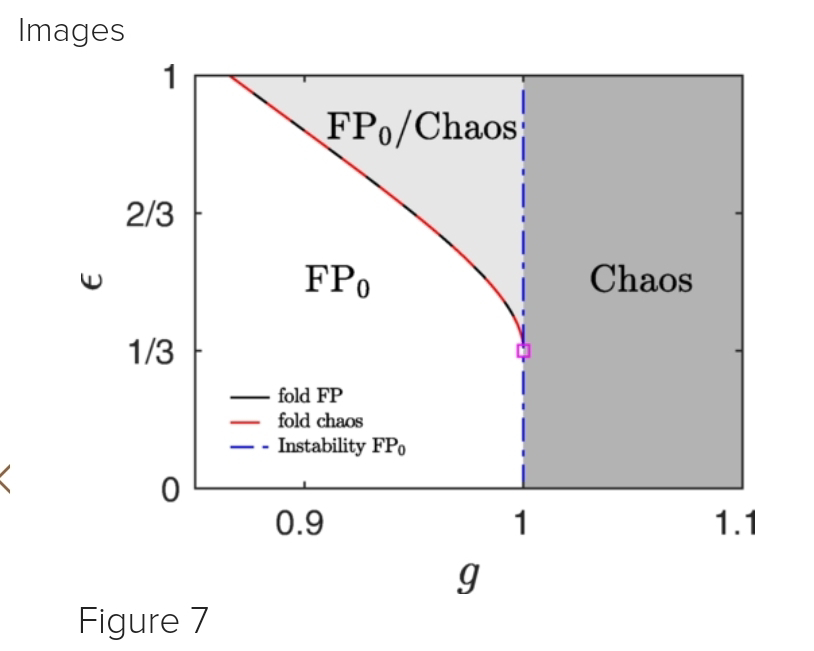
AA << study a paradigmatic random recurrent neural network introduced by Sompolinsky, Crisanti, and Sommers (SCS). In the infinite size limit, this system exhibits a direct transition from a homogeneous rest state to chaotic behavior, with the Lyapunov exponent gradually increasing from zero. (AA)  generalize the SCS model considering odd saturating nonlinear transfer functions, beyond the usual choice 𝜙⁡(𝑥)=tanh⁡𝑥. A discontinuous transition to chaos occurs whenever the slope of 𝜙 at 0 is a local minimum [i.e., for 𝜙′′′⁢(0)>0]. Chaos appears out of the blue, by an attractor-repeller fold. Accordingly, the Lyapunov exponent stays away from zero at the birth of chaos. >>

In the figure 7 << the pink square is located at the doubly degenerate point (𝑔,𝜀)=(1,1/3). >>️️

Diego Pazó. Discontinuous transition to chaos in a canonical random neural network. Phys. Rev. E 110, 014201. July 1, 2024.

https://journals.aps.org/pre/abstract/10.1103/PhysRevE.110.014201

Also: chaos, random, network, transition, neuro, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, chaos, random, network, transition, neuro

# gst: the hypothesis of the onset of extreme events via an attractor merging crisis.

AA << investigate the temporal dynamics of the Ikeda Map with Balanced Gain and Loss and in the presence of feedback loops with saturation nonlinearity. From the bifurcation analysis, (They) find that the temporal evolution of optical power undergoes period quadrupling at the exceptional point (EP) of the system and beyond that, chaotic dynamics emerge in the system and this has been further corroborated from the Largest Lyapunov Exponent (LLE) of the model. >>

<< For a closer inspection, (AA) analyzed the parameter basin of the system, which further leads to (their) inference that the Ikeda Map with Balanced Gain and Loss exhibits the emergence of chaotic dynamics beyond the exceptional point (EP). >>

<< Furthermore, (AA) find that the temporal dynamics beyond the EP regime leads to the onset of Extreme Events (EE) in this system via attractor merging crisis. >>️

Jyoti Prasad Deka, Amarendra K. Sarma. Temporal Dynamics beyond the Exceptional Point in the Ikeda Map with Balanced Gain and Loss. arXiv: 2406.17783 [eess.SP]. May 13, 2024. 

https://arxiv.org/abs/2406.17783 

Also: chaos, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, chaos, chaotic dynamics, attractor merging crisis 

# gst: when generalized diffusion could result from stochastic processes.

<< Despite the success of fractional Brownian motion (fBm) in modeling systems that exhibit anomalous diffusion due to temporal correlations, recent experimental and theoretical studies highlight the necessity for a more comprehensive approach of a generalization that incorporates heterogeneities in either the tracers or the environment. >>

AA present << a modification of Lévy's representation of fBm for the case in which the generalized diffusion coefficient is a stochastic process. (They) derive analytical expressions for the autocovariance function and both ensemble- and time-averaged mean squared displacements. Further, (AA)  validate the efficacy of the developed framework in two-state systems, comparing analytical asymptotic expressions with numerical simulations. >>️

Adrian Pacheco-Pozo, Diego Krapf. Fractional Brownian motion with fluctuating diffusivities. Phys. Rev. E 110, 014105. Jul 1, 2024.

https://journals.aps.org/pre/abstract/10.1103/PhysRevE.110.014105

Also: disorder, fluctuations, network, transition, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, fractional Brownian motion, fBm, Lévy, disorder, fluctuations, anomalous, network, transition

# gst: the strangeness of networks, the hypothesis of a connection between the kinetics of networks and anomalous transport theory.

<< Many real-world networks change over time. Think, for example, of social interactions, gene activation in a cell, or strategy making in financial markets, where connections and disconnections occur all the time. >>

AA team << has gained groundbreaking insights into this problem by recasting the discrete dynamics of a network as a continuous time series (..). In doing so, the researchers have discovered that if the breaking and forming of links are represented as a particle moving in a suitable geometric space, then its motion is subdiffusive—that is, slower than it would be if it diffused normally. What’s more, the particles’ motions are well described by fractional Brownian motion, a generalization of Einstein’s classic model. This feat establishes a profound connection between the kinetics of time-varying or “temporal” networks and anomalous transport theory, opening fresh prospects for developing predictive equations of motion for networks. >>️

Ivan Bonamassa. Strange Kinetics Shape Network Growth. Physics 17, 96. Jun 17, 2024.

https://physics.aps.org/articles/v17/96

Evangelos S. Papaefthymiou, Costas Iordanou, Fragkiskos Papadopoulos. Fundamental Dynamics of Popularity-Similarity Trajectories in Real Networks. Phys. Rev. Lett. 132, 257401. Jun 17, 2024. 

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.132.257401

Also: network, transition, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, network, transition

# gst: chaos creates and destroys branched flows.

<< Electrons, lasers, tsunamis, and ants have at least one thing in common: they all display branched flow. Whenever a wave propagates through a weakly refracting medium, flow is expected to accumulate along certain directions, forming structures called branches. >>️

AA << explore the laws governing the evolution of the branches in periodic potentials. On one hand, (They) observe that branch formation follows a similar pattern in all non-integrable potentials, no matter whether the potentials are periodic or completely irregular. Chaotic dynamics ultimately drives the birth of the branches. On the other hand, (AA) results reveal that for periodic potentials the decay of the branches exhibits new characteristics due to the presence of infinitely stable branches known as superwires.  >>️

Alexandre Wagemakers, Aleksi Hartikainen, et al. Chaotic dynamics creates and destroys branched flow. arXiv: 2406.12922v1 [nlin.PS]. Jun 14, 2024. 

https://arxiv.org/abs/2406.12922

Also: chaos, transition, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, chaos, transition, branched flows, superwires 

# ai: apropos of Black Box in Generative Artificial Intelligence, the scientific XAI.

<< The scientific method is the cornerstone of human progress across all branches of the natural and applied sciences, from understanding the human body to explaining how the universe works. The scientific method is based on identifying systematic rules or principles that describe the phenomenon of interest in a reproducible way that can be validated through experimental evidence. In the era of artificial intelligence (AI), there are discussions on how AI systems may discover new knowledge. >>

<< More specifically, knowing what data AI systems used to make decisions can be a point of contact with domain experts and scientists, that can lead to divergent or convergent views on a given scientific problem. Divergent views may spark further scientific investigations leading to new scientific knowledge. Convergent views may instead reassure that the AI system is operating within bounds deemed reasonable to humans. >>️

<< The perspective (AA) present here was inspired by several authors that published on the topic of AI for science in the past few years, but perhaps one contribution stands out: the inspiring New York Times editorial by Steven Strogatz (Strogatz, S. One giant step for a chess-playing machine. New York Times 26 (2018)) covering the winning of AlphaZero against Stockfish. In that piece, Strogatz states: “What is frustrating about machine learning, however, is that the algorithms can’t articulate what they’re thinking. We don’t know why they work, so we don’t know if they can be trusted. AlphaZero gives every appearance of having discovered some important principles about chess, but it can’t share that understanding with us.”. He additionally cites Garry Kasparov (the former world chess champion) that stated: “we would say that its [AlphaZero] style reflects the truth. This superior understanding allowed it to outclass the world’s top traditional program despite calculating far fewer positions per second.” >>️

AA highlights the importance of three aspects regarding scientific XAI (explainable Artificial Intelligence): accuracy, reproducibility, understandability, ️

Apropos of 'understandability', << The machine view should be understandable to scientists and domain experts. (..) If we want a scientist to make sense of the data used by a machine, this data should contain viable features that allow a scientist to tap into its existing corpus of knowledge. >>

<< XAI may also alleviate some of the risks that we may face when using AI for scientific discovery, that we share with Messeri and Crockett (‘adopting AI in scientific research can bind to our cognitive limitations and impede scientific understanding despite promising to improve it’). >>

️

Gianmarco Mengaldo. Explain the Black Box for the Sake of Science: Revisiting the Scientific Method in the Era of Generative Artificial Intelligence. arXiv: 2406.10557v1 [cs.AI]. Jun 15, 2024.

https://arxiv.org/abs/2406.10557

Also: ai (artificial intell), in https://www.inkgmr.net/kwrds.html 

Keywords: AI, XAI, Artificial Intelligence

# gst: buckling instability in a chain of sticky bubbles

<< A slender object undergoing an axial compression will buckle to alleviate the stress. Typically the morphology of the deformed object depends on the bending stiffness for solids, or the viscoelastic properties for liquid threads. >>️

AA << study a chain of uniform sticky air bubbles that rise due to buoyancy through an aqueous bath. A buckling instability of the bubble chain with a characteristic wavelength is observed.  >>️

<< If a chain of bubbles is produced faster than it is able to rise, the dominance of viscous drag over buoyancy results in a compressive stress that is alleviated by buckling the bubble chain. >>️

<< Unlike other systems, in which buckling arises from a cost associ­ated with bending, to our knowledge this is the first study of drag-induced buckling with no intrinsic cost to bending—a buckling instability with a characteristic lengthscale emerges as a result of hydrodynamics. >>

️

Carmen L. Lee and Kari Dalnoki-Veress. Buckling instability in a chain of sticky bubbles. Phys. Rev. Research 6, L022062. Jun 14, 2024. 

https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.6.L022062

Also: bubble, instability, transition, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, bubble, instability, drop, droplet, droploid, transition