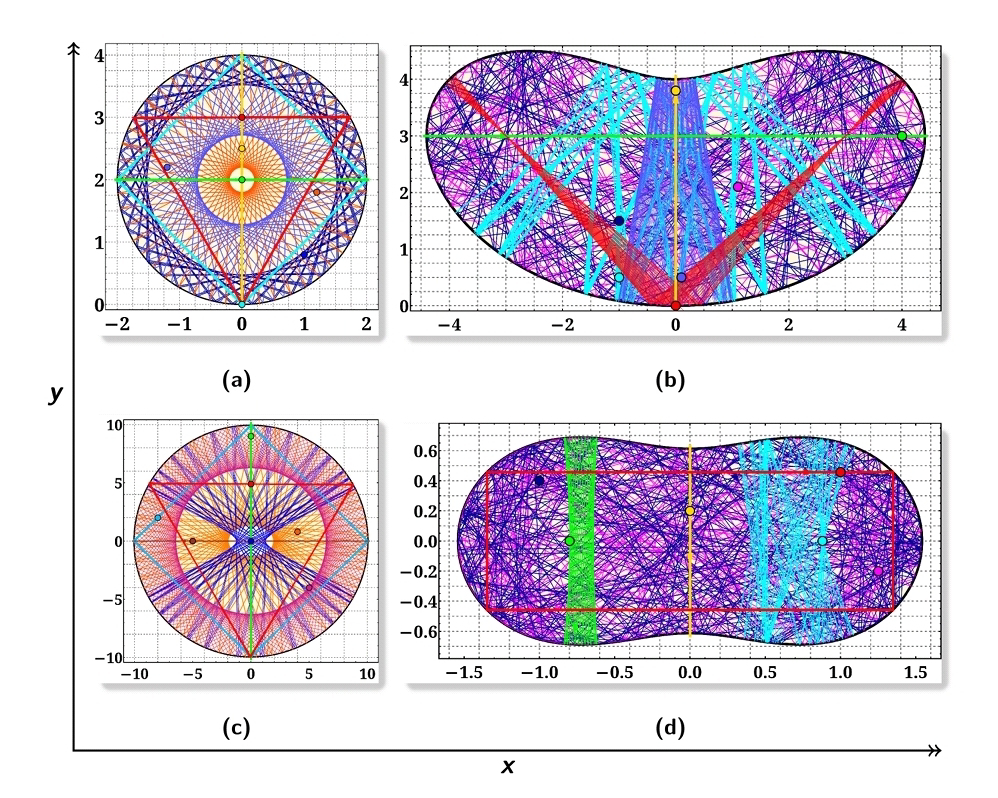
# gst: chaotic billiards inside mixed curvatures

<< The boundary of a billiard system dictates its dynamics, which can be integrable, mixed, or fully chaotic. >>️

This AA study << introduces two such billiards: a bean-shaped billiard and a peanut-shaped billiard, the latter being a variant of Cassini ovals. Unlike traditional chaotic billiards, these systems incorporate both focusing and defocusing regions along their boundaries, with no neutral segments. >>

AA << examine both classical and quantum dynamics of these billiards and observe a strong alignment between the two perspectives. For classical analysis, the billiard flow diagram and billiard map reveal sensitivity to initial conditions, a hallmark of classical chaos. In the quantum domain, (AA) use nearest-neighbour spacing distribution and spectral complexity as statistical measures to characterise chaotic behaviour. >>

<< Both classical and quantum mechanical analysis are in firm agreement with each other. One of the most striking quantum phenomena (They) observe is the eigenfunction scarring (both scars and super-scars). Scarring phenomena serve as a rich visual manifestation of quantum and classical correspondence, and highlight quantum suppression chaos at a local level. >>

Pranaya Pratik Das, Tanmayee Patra, Biplab Ganguli. Manifestations of chaos in billiards: the role of mixed curvature. arXiv: 2501.08839v1 [nlin.CD]. Jan 15, 2025.

https://arxiv.org/abs/2501.08839

Also: billiard, chaos, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, billiard, chaos

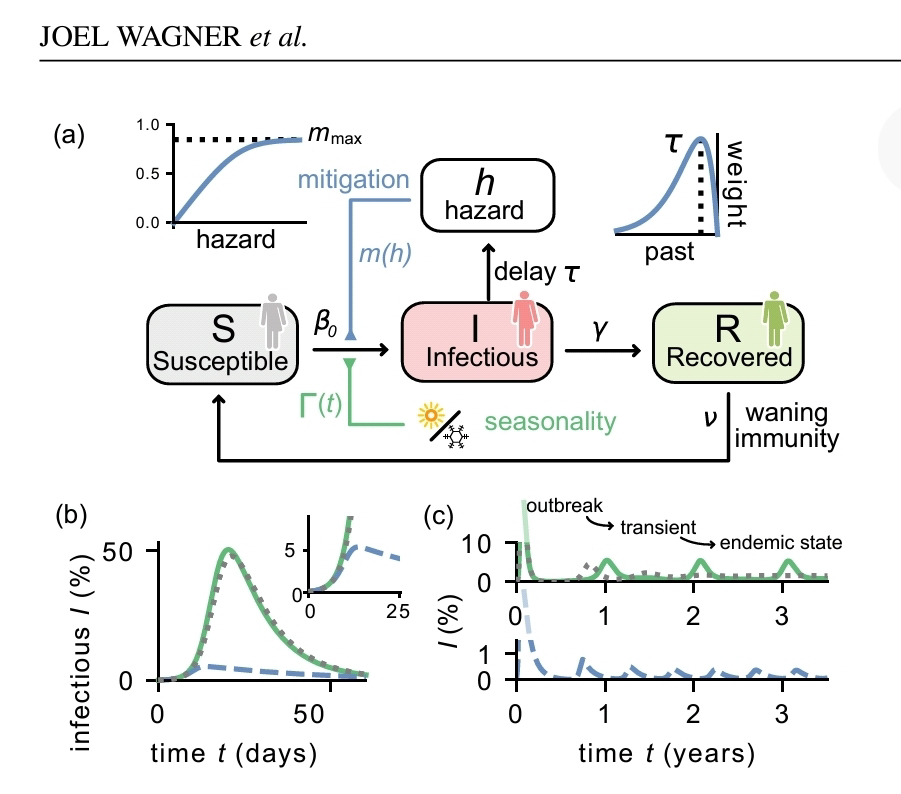
# epidem: societal self-regulation appears to induce complex infection dynamics and chaos.

<< Classically, endemic infectious diseases are expected to display relatively stable, predictable infection dynamics. Accordingly, basic disease models such as the susceptible-infected-recovered-susceptible model display stable endemic states or recurrent seasonal waves. However, if the human population reacts to high infection numbers by mitigating the spread of the disease, then this delayed behavioral feedback loop can generate infection waves itself, driven by periodic mitigation and subsequent relaxation. >>

AA << show that such behavioral reactions, together with a seasonal effect of comparable impact, can cause complex and unpredictable infection dynamics, including Arnold tongues, coexisting attractors, and chaos. >>

<< Importantly, these arise in epidemiologically relevant parameter regions where the costs associated to infections and mitigation are jointly minimized. By comparing (Their) model to data, (AA) find signs that COVID-19 was mitigated in a way that favored complex infection dynamics. (AA)  results challenge the intuition that endemic disease dynamics necessarily implies predictability and seasonal waves and show the emergence of complex infection dynamics when humans optimize their reaction to increasing infection numbers. >>️

Joel Wagner, Simon Bauer, et al.  Societal self-regulation induces complex infection dynamics and chaos. Phys. Rev. Research 7, 013308. Mar 24, 2025.

https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.7.013308

Also: virus, sars* covid* (aka 1or2achoos), waves, chaos, in https://www.inkgmr.net/kwrds.html 

Keywords: epidemiology, virus, sars, covid-19, chaos

# gst: chaotic dynamics modulate complex systems, even in the presence of extrinsic and intrinsic noise

AA << find that chaotic dynamics modulates gene expression and up-regulates certain families of low-affinity genes, even in the presence of extrinsic and intrinsic noise. Furthermore, this leads to an increase in the production of protein complexes and the efficiency of their assembly. Finally, (AA) show how chaotic dynamics creates a heterogeneous population of cell states, and describe how this can be beneficial in multi-toxic environments. >>

Mathias L. Heltberg, Sandeep Krishna, Mogens H. Jensen. On chaotic dynamics in transcription factors and the associated effects in differential gene regulation.  Nature Comm. volume 10, Article number: 71 Jan 8, 2019.   https://www.nature.com/articles/s41467-018-07932-1  

<< Chaos in bodily regulation can optimize our immune system according to a recent discovery made by researchers at the University of Copenhagen's Niels Bohr Institute. The discovery may prove to be of great significance for avoiding serious diseases such as cancer and diabetes.  >>

Chaos in the body tunes up your immune system. Niels Bohr Institute.
Jan 16, 2019.   https://m.medicalxpress.com/news/2019-01-chaos-body-tunes-immune.html

Also

'l'immaginifico "tracciante ... che svagola nella macina ...'    in:  2149 - onda di predazione (to knock seals off the ice). Notes. Dec 17, 2007.    https://inkpi.blogspot.com/2007/12/2149-onda-di-predazione-to-knock-seals.html

Also

never boring with chaos and tit-for-tat theories. F.on.T. Jun 12, 2016.  https://flashontrack.blogspot.com/2016/06/s-gst-never-boring-with-chaos-and-tit.html

# gst: limit cycles and chaos in planar hybrid systems.

<< The main inspiration of (this AA) work is the paper of Llibre and Teixeira (Nonlinear Dyn. 91, No. 1, 249-255, 2018) about Filippov systems formed by two linear centers and having x = 0 as discontinuity line. One of the main conclusions of the paper is that such systems cannot have limit cycles. Actually, either it does not have periodic orbits or every orbit is periodic. Therefore, its dynamics is relatively simple. Inspired by this work and the raising notion of hybrid systems, (AA) wondered what could happen if we allow jumps on the discontinuity line. As a result, (They) discovered not only that limit cycles are allowed with arbitrarily small “perturbations” in the jump, (..), but also that such systems allow chaotic dynamics. Therefore, (AA) conclude that hybrid systems with simple formulation can have rich dynamics. (They) also observe that a complete characterization of the dynamics of X ∈ Xn depends on the characterization of its first return map, which is a piecewise polynomial map on the real line. This, together with the fact that the systems studied here are a generalization of the Filippov systems (..), illustrates that hybrid systems can be seen as a three-fold bridge connecting continuous, piecewise continuous and discrete dynamical systems. >>️

Jaume Llibre, Paulo Santana. Limit cycles and chaos in planar hybrid systems. arXiv: 2407.05151v2 [math.DS]. Oct 1, 2024. 

https://arxiv.org/abs/2407.05151

Also: chaos, transition, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, limit cycles, chaos, transitions, small perturbations, jumps  

# gst: a chaos-inducing approach against superbugs evolution

<< The CHAOS [Controlled Hindrance of Adaptation of OrganismS] method takes advantage of this effect, pulling multiple genetic levers in order to build up stress on the bacterial cell and eventually trigger a cascading failure, leaving the bug more vulnerable to current treatments. The technique does not alter the bug's DNA itself, only the expression of individual genes, similar to the way a coded message is rendered useless without the proper decryption. >>

<< We now have a way to cut off the evolutionary pathways of some of the nastiest bugs and potentially prevent future bugs from emerging at all, >> Peter Otoupal

Chaos-inducing genetic approach stymies antibiotic-resistant superbugs. University of Colorado at Boulder. Sept 3, 2018.

https://m.phys.org/news/2018-09-chaos-inducing-genetic-approach-stymies-antibiotic-resistant.html 

<< While individual perturbations improved fitness during antibiotic exposure, multiplexed perturbations caused large fitness loss in a significant epistatic fashion. >>

Peter B. Otoupal, William T. Cordell, et al. Multiplexed deactivated CRISPR-Cas9 gene expression perturbations deter bacterial adaptation by inducing negative epistasis. Comm  Biol 1 (129) Sept 3, 2018

https://www.nature.com/articles/s42003-018-0135-2

# gst: even tight-binding billiards could exhibit chaotic behaviors

<< Recent works have established universal entanglement properties and demonstrated validity of single-particle eigenstate thermalization in quantum-chaotic quadratic Hamiltonians. However, a common property of all quantum-chaotic quadratic Hamiltonians studied in this context so far is the presence of random terms that act as a source of disorder. >>

AA << introduce tight-binding billiards in two dimensions, which are described by non-interacting spinless fermions on a disorder-free square lattice subject to curved open boundaries. >>

They <<  show that many properties of tight-binding billiards match those of quantum-chaotic quadratic Hamiltonians (..) these properties indeed appear to be consistent with the emergence of quantum chaos in tight-binding billiards. This statement nevertheless needs to be taken with some care since there exist a sub-extensive (in lattice volume) set of single-particle eigenstates that are degenerate in the middle of the spectrum at zero energy (i.e., zero modes), for which the agreement with RMT (random matrix theory) predictions may not be established. >>

Iris Ulcakar, Lev Vidmar. Tight-binding billiards. arXiv:2206.07078v1 [cond-mat.stat-mech]. Jun 14, 2022. 

https://arxiv.org/abs/2206.07078

Also

keyword 'billiard' in FonT

https://flashontrack.blogspot.com/search?q=billiard

keyword 'chaos' | 'chaotic' in Font

https://flashontrack.blogspot.com/search?q=chaos

https://flashontrack.blogspot.com/search?q=chaotic

keyword 'caos' | 'caotico' in Notes (quasi-stochastic poetry)

https://inkpi.blogspot.com/search?q=caos

https://inkpi.blogspot.com/search?q=caotico

keywords: gst, billiard, chaos, chaotic behavior

# gst: elasticity of fibres prefers the chaos of turbulence.

FIG. 4. Maximal Lyapunov exponents λ1 associated with the flow regions sampled by the fibre centre of masses in a 3D turbulent flow. 

<< Turbulent flows are ubiquitous in nature and are responsible for numerous transport phenomena that help sustain life on earth. >>️

AA << have shown that the stretching of fibres is due only to elasticity and their inertia playing a minimal role as they are advected by a turbulent carrier flow. A highly elastic fibre is much more likely to be stretched out and as a result prefers a “straighter” configuration rather than a coiled one. >>️

<< These inertial, elastic fibres then exhibit non-trivial preferential sampling of a 3D turbulent flow in a manner qualitatively similar to 2D turbulence (..). Inertia leads fibres away from vortical regions while their elasticity pulls them inside the vortices. Upto a moderate inertia (St ∼ O(1)), fibres increasingly prefer the straining regions of the flow, while at much larger inertia (St ≫ 1) they decorrelate from the flow and preference for straining regions begins to diminish again. >>️

<< However, owing to a large elasticity, fibres get trapped in vortical regions (at small St), as well as are unable able to exit the straining regions quickly. A more elastic and extensible fibre is, thus, more likely to spend longer times in both vortical and the straining regions of the flow. >>️

<< This picture of preferential sampling of a 3D turbulent flow by elastic, inertial fibres is also confirmed by alternately studying the chaoticity of the sampled flow regions via Lyapunov Exponents. Less elastic fibres prefer less chaotic (vortical) regions of the flow while more chaotic (straining) regions are preferred at large Wi. LEs also confirm that preferential sampling has a non-monotonic dependence on St for small elasticity but which is lost when Wi becomes very large.  >>

<< It would (..) be even more interesting to see how chaotic the fibre trajectories themselves are and what that has to say about fibre dynamics in turbulent flows. >>️

️

Rahul K. Singh. Elasticity of fibres prefers the chaos of turbulence. arXiv: 2406.06033v1. Jun 10, 2024.

https://doi.org/10.48550/arXiv.2406.06033

Also: elastic, chaos, turbulence, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, elastic, chaos, turbulence

# gst: isles of regularity (depending on the initial setup) in a sea of chaos amid the gravitational three-body problem.

AA << study probes the presence of regular (i.e. non-chaotic) trajectories within the 3BP (three-body problem) and assesses their impact on statistical escape theories. >>

AA << analysis reveals that regular trajectories occupy a significant fraction of the phase space, ranging from 28% to 84% depending on the initial setup, and their outcomes defy the predictions of statistical escape theories. The coexistence of regular and chaotic regions at all scales is characterized by a multi-fractal behaviour. >>

Alessandro Alberto Trani, Nathan W.C. Leigh, et al. Isles of regularity in a sea of chaos amid the gravitational three-body problem. A&A, 689, A24, Jun 25, 2024.

https://www.aanda.org/articles/aa/full_html/2024/09/aa49862-24/aa49862-24.html

"Islands" of Regularity Discovered in the Famously Chaotic Three-Body Problem. University of Copenhagen. Oct 11, 2024.

https://science.ku.dk/english/press/news/2024/islands-of-regularity-discovered-in-the-famously-chaotic-three-body-problem/

Also: three balls, escape, chaos, transition, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, three balls, escape, chaos, transition 

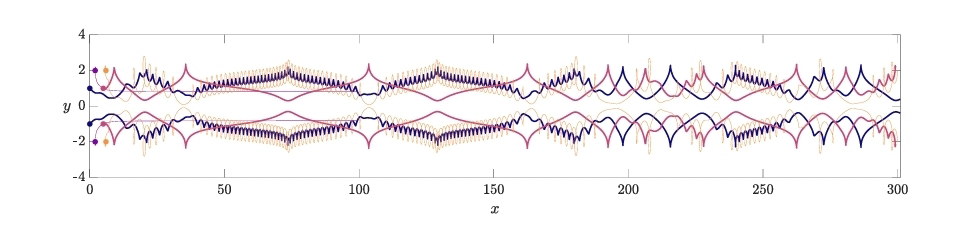
# gst: self-feedback delay induces extreme events in the theoretical Brusselator system.

AA << ️present a study of the theoretical Brusselator model with time-delayed self-feedback, demonstrating its ability to induce extreme events when delays in reaction processes significantly influence subsequent dynamics, with and without diffusion. >>

<< ️Stability analyses reveal the mechanisms driving this behavior with respect to the delay time. The occurrence of extreme events is validated using various numerical and statistical tools, including phase portraits, time series, probability distribution functions, return periods, and spatiotemporal evolution. >>

<< ️A comprehensive two-parameter scan delineates the parameter regimes where the extreme events emerge, alongside the identification of transient chaos within specific regions of the parameter space. To confirm these numerical findings, (AA) constructed an analog electronic circuit that emulates the model, providing experimental validation of the predicted dynamics. >>

S. V. Manivelan, S. Sabarathinam, et al. Self-feedback delay induces extreme events in the theoretical Brusselator system. Phys. Rev. E 112, 014202. Jul 1, 2025.

https://journals.aps.org/pre/abstract/10.1103/v1h2-42w1

Also: chaos, transition, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, Brusselator system, self-feedback, delay, chaos, transient chaos, transitions, extreme events.

# gst: order and chaos in systems of coaxial vortex pairs

Fig. B.12: Ex. with 4 interact. vortex pairs

AA << have analyzed interactions between two and three coaxial vortex pairs, classifying their dynamics as either ordered or chaotic based on strengths, initial sizes, and initial horizontal separations.  >>️

They << found that periodic cases are scattered among chaotic ones across different initial configurations. Quasi-periodic leapfrogging typically occurs when the initial distances between the vortex pairs are small and cannot coexist with vortex-pair overtake. When the initial configuration splits into two interacting vortex pairs and a single propagating vortex pair, the two interacting pairs consistently exhibit periodic leapfrogging. For the smallest initial horizontal separations, the system predominantly exhibits chaotic or quasi-periodic motions rather than periodic leapfrogging with a single frequency. This behavior is due to the strong coupling between all three vortex pairs. When the pairs are in close proximity, more complex and chaotic dynamics emerge instead of periodic motion. >>

Their << findings indicate that quasi-periodic leapfrogging and chaotic interactions generally occur when the three vortex pairs have similar strengths and initial sizes. Conversely, discrepancies in these parameters cause the system to disintegrate into two subsystems: a single propagating vortex pair and two periodically leapfrogging pairs. >>️

️

Christiana Mavroyiakoumou, Wenzheng Shi. Order and Chaos in Systems of Coaxial Vortex Pairs. arXiv: 2502.07002v1 [physics.flu-dyn]. Feb 10, 2025. ️

https://arxiv.org/abs/2502.07002

Also: chaos, vortex, order, disorder, disorder & fluctuations, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, chaos, vortex, order, disorder, disorder & fluctuations

# gst: reshaping Kuramoto model, when a collective dynamics becomes chaotic, with a surprisingly weak coupling.

<< The emergence of collective synchrony from an incoherent state is a phenomenon essentially described by the Kuramoto model (..) Collective synchronization is a phenomenon in which an ensemble of heterogeneous, self-sustained oscillatory units (commonly known as oscillators) spontaneously entrain their rhythms. This is a pervasive phenomenon observed in natural systems and man-made devices, covering a wide range of spatio-temporal scales, from cell aggregates to swarms of fireflies >>

<< However, this is only partly true, (..) Kuramoto’s perturbative phase-reduction approach is valid for weak coupling. Specifically, oscillator heterogeneity and interactions appear at zeroth and linear orders in the coupling constant, respectively. >> 

AA << have introduced the ‘enlarged Kuramoto model’; a population of phase oscillators in which three-body interactions enter in a perturbative way. Remarkably, this makes a world of difference, drastically reshaping the traditional Kuramoto scenario. The ‘enlarged Kuramoto model’ exhibits a variety of unsteady states, including collective chaos and hyperchaos. >>

Ivan Leon, Diego Pazo. Enlarged Kuramoto Model: Secondary Instability and Transition to Collective Chaos. arXiv: 2112.00176v1 [nlin.AO]. Nov 30, 2021.

https://arxiv.org/abs/2112.00176

Also

More on the three-body problem (695 families of collisionless orbits). FonT. Oct 16, 2017. 

https://flashontrack.blogspot.com/2017/10/gst-more-on-three-body-problem-695.html

Keywords: gst, behav, instability, Kuramoto model, three-body interactions, chaos, collective chaos, hyperchaos.

# gst: synchronization and chaos in complex systems with delayed interactions.

<< Explaining the wide range of dynamics observed in ecological communities is challenging due to the large number of species involved, the complex network of interactions among them, and the influence of multiple environmental variables. >>

AA << consider a general framework to model the dynamics of species-rich communities under the effects of external environmental factors, showing that it naturally leads to delayed interactions between species, and analyze the impact of such memory effects on population dynamics. >>

<< Employing the generalized Lotka-Volterra equations with time delays and random interactions, (AA) characterize the resulting dynamical phases in terms of the statistical properties of community interactions. (Their) findings reveal that memory effects can generate persistent and synchronized oscillations in species abundances in sufficiently competitive communities. This provides an additional explanation for synchronization in large communities, complementing known mechanisms such as predator-prey cycles and environmental periodic variability. >>

<< Furthermore, (AA) show that when reciprocal interactions are negatively correlated, time delays alone can induce chaotic behavior. This suggests that ecological complexity is not a prerequisite for unpredictable population dynamics, as intrinsic memory effects are sufficient to generate long-term fluctuations in species abundances. >>

Francesco Ferraro, Christian Grilletta, et al. Synchronization and chaos in complex ecological communities with delayed interactions. arXiv: 2503.21551v1 [q-bio.PE]. Mar 27, 2025.

https://arxiv.org/abs/2503.21551

Also: pause, silence, random, chaos, network, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, pause, silence, random, chaos, chaotic behavior, network, delay, time delay, delayed interactions, random interactions, memory effect 

# gst: unstable fixed points in chaotic networks

<< Understanding the high-dimensional chaotic dynamics occurring in complex biological systems such as recurrent neural networks or ecosystems remains a conceptual challenge. For low-dimensional dynamics, fixed points provide the geometric scaffold of the dynamics. However, in high-dimensional systems, even the location of fixed points is unknown. >>

Here, AA << analytically determine the number and distribution of fixed points for a canonical model of a recurrent neural network that exhibits high-dimensional chaos. This distribution reveals that fixed points and dynamics are confined to separate shells in state space. Furthermore, the distribution enables (AA) to determine the eigenvalue spectra of the Jacobian at the fixed points, showing that each fixed point has a low-dimensional unstable manifold. >>

<< Despite the radial separation of fixed points and dynamics, (They)  find that the principal components of fixed points and dynamics align and that nearby fixed points act as partially attracting landmarks for the dynamics. >>

AA results << provide a detailed characterization of the fixed point geometry and its interplay with the dynamics, thereby paving the way towards a geometric understanding of high-dimensional chaos through their skeleton of unstable fixed points. >>

Jakob Stubenrauch, Christian Keup, et al. Fixed point geometry in chaotic neural networks. Phys. Rev. Research 7, 023203. May 29, 2025.

https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.7.023203

Also: chaos, disorder & fluctuations, instability, transition, network, brain, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, chaos, networks, neural networks, ecosystems, fixed points, unstable fixed points.

# gst: networks of pendula with diffusive interactions, chaotic regime seems to emerge at low energies.

AA << study a system of coupled pendula with diffusive interactions, which could depend both on positions and on momenta. The coupling structure is defined by an undirected network, while the dynamic equations are derived from a Hamiltonian; as such, the energy is conserved. >>️

<< The behaviour observed showcases a mechanism for the appearance of chaotic oscillations in conservative systems. For Hamiltonians with two degrees of freedom, it has been shown how chaos can emerge near a saddle-centre equilibrium possessing a homoclinic orbit. (AA) have seen that higher-dimensional systems having mixed equilibria, i.e., generalisations of a saddle-center where the eigenvalues are only imaginary and reals, also show chaotic behaviour close to those points.  >>️

AA << complement the analysis with some numerical simulations showing the interplay between bifurcations of the origin and transitions to chaos of nearby orbits. A key feature is that the observed chaotic regime emerges at low energies. >>

️

Riccardo Bonetto, Hildeberto Jardón-Kojakhmetov, Christian Kuehn. Networks of Pendula with Diffusive Interactions. arXiv: 2408.02352v1 [math.DS]. Aug 5, 2024.

https://arxiv.org/abs/2408.02352

Also: pendulum, network, transition, chaos, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, pendulum, network, transition, chaos, bifurcation

# gst: evolving disorder and chaos induces acceleration of elastic waves.

<< Static or frozen disorder, characterised by spatial heterogeneities, influences diverse complex systems, encompassing many-body systems, equilibrium and nonequilibrium states of matter, intricate network topologies, biological systems, and wave-matter interactions. >>

AA << investigate elastic wave propagation in a one-dimensional heterogeneous medium with diagonal disorder. (They) examine two types of complex elastic materials: one with static disorder, where mass density randomly varies in space, and the other with evolving disorder, featuring random variations in both space and time. (AA) results indicate that evolving disorder enhances the propagation speed of Gaussian pulses compared to static disorder. Additionally, (They) demonstrate that the acceleration effect also occurs when the medium evolves chaotically rather than randomly over time. The latter establishes that evolving randomness is not a unique prerequisite for observing wavefront acceleration, introducing the concept of chaotic acceleration in complex media. >>️

M. Ahumada, L. Trujillo, J. F. Marín. Evolving disorder and chaos induces acceleration of elastic waves. arXiv: 2403.02113v1 [cond-mat.dis-nn]. Mar 4, 2024. 

https://arxiv.org/abs/2403.02113

Also: waves, elastic, chaos, transition, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, waves, elastic, chaos, transition

# gst: elasticity of fibers prefers the chaos of turbulence.

<< The dynamics of fibers, modeled as a sequence of inertial beads linked via elastic springs, in turbulent flows is dictated by a nontrivial interplay of inertia and elasticity. Such elastic, inertial fibers preferentially sample a three-dimensional turbulent flow in a manner that is qualitatively similar to that in two dimensions [R. Singh et al., Phys. Rev. E 101, 053105 (2020)]. >>

<< Both these intrinsic features have competing effects on fiber dynamics: Inertia drives fibers away from vortices while elasticity tends to trap them inside. However, these effects swap roles at very large values. A large inertia makes the fibers sample the flow more uniformly while a very large elasticity facilitates the sampling of straining regions. >>

<< This complex sampling behavior is further corroborated by quantifying the chaotic nature of sampled flow regions. This is achieved by evaluating the maximal Lagrangian Lyapunov Exponents associated with the flow along fiber trajectories. >>

Rahul K. Singh. Elasticity of fibers prefers the chaos of turbulence. Phys. Rev. E 111, L053101. May 5, 2025.

https://journals.aps.org/pre/abstract/10.1103/PhysRevE.111.L053101

Also: elastic, turbulence, chaos, transition, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, elasticity, turbulence, chaos, transitions

# brain: actually there is chaos in the brain

<< Besides some empirical findings of chaos at different time scales, the focus is on theoretical modeling of change processes explaining and simulating chaotic dynamics. It will be illustrated how some common factors of psychotherapeutic change and psychological hypotheses on motivation, emotion regulation, and information processing of the client's functioning can be integrated into a comprehensive nonlinear model of human change processes >>

Schiepek GK, Viol K, et al. Psychotherapy Is Chaotic - (Not Only) in a Computational World. Front Psychol. 2017 Apr 24;8:379. doi: 10.3389/fpsyg.2017.00379. eCollection 2017.

https://www.ncbi.nlm.nih.gov/m/pubmed/28484401/

<< Cambridge-based researchers provide new evidence that the human brain lives "on the edge of chaos", at a critical transition point between randomness and order. The study provides experimental data on an idea previously fraught with theoretical speculation >>

Public Library of Science. The Human Brain Is On The Edge Of Chaos. Mar 23, 2009.

https://www.sciencedaily.com/releases/2009/03/090319224532.htm  

Manfred G. Kitzbichler, Marie L. Smith, et al. Broadband Criticality of Human Brain Network Synchronization. PLoS Comput Biol 2009; 5 (3): e1000314. doi: 10.1371/journal.pcbi.1000314. Mar 20, 2009.

http://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1000314

# gst: approaching chaotic dynamics to trace the complexity of rough nanostructured surfaces

AA << use the basic ingredients of chaotic dynamics (stretching and folding of phase space points) for the characterization of the complexity of microscopy images of rough surfaces. The key idea is to use an image as the initial condition of a chaotic discrete dynamical system, such as the Arnold cat map, and track its transformations during the first iterations of the map. Since the basic effects of the Arnold map are the stretching and folding of image texture, the application of the map leads to an enhancement of the high frequency content of images along with an increase of discontinuities in pixel intensities. (AA) exploit these effects to quantify the complexity of S type (lying between homogeneity and randomness) of the image texture since the first (enhancement of high frequencies) can be used to quantify the distance of texture from randomness and noise and the second (the proliferation of discontinuities) the distance from order and homogeneity. The method is validated in synthetic images which are generated from computer generated surfaces with controlled correlation length and fractal dimension and it is applied in real images of nanostructured surfaces obtained from a scanning electron microscope with very interesting results. >>️

A. Kondi, V. Constantoudis, P. Sarkiris, K. Ellinas, and E. Gogolides. Using chaotic dynamics to characterize the complexity of rough surfaces. Phys. Rev. E 107, 014206. Jan 11, 2023. 

https://journals.aps.org/pre/abstract/10.1103/PhysRevE.107.014206

https://twitter.com/PhysRevE/status/1613569770338533376

Also

Able to track changes in noise. 

(quasi-stochastic poetry) 

Notes. Sep 13, 2007. 

https://inkpi.blogspot.com/2007/09/2147-able-to-track-changes-in-noise.html

Also

keyword 'chaos' | 'chaotic' in Font

https://flashontrack.blogspot.com/search?q=chaos

https://flashontrack.blogspot.com/search?q=chaotic

keyword 'caos' | 'caotico' in Notes (quasi-stochastic poetry)

https://inkpi.blogspot.com/search?q=caos

https://inkpi.blogspot.com/search?q=caotico

Keywords: gst, chaos, chaotic, nano, roughness, wetting, surfaces, etching scanning 

# gst: chaos from a double pendulum

<< Three double pendulums, all starting with near identical initial conditions, all rapidly diverging. >>

Ari Rubinsztejn. Chaos and the Double Pendulum. Nov 19, 2018.

https://gereshes.com/2018/11/19/chaos-and-the-double-pendulum

# gst: scrambling does not necessitate chaos.

<< Focusing on semiclassical systems, (AA) show that the parametrically long exponential growth of out-of-time order correlators (OTOCs), also known as scrambling, does not necessitate chaos. Indeed, scrambling can simply result from the presence of unstable fixed points in phase space, even in an integrable model. >>

Tianrui Xu, Thomas Scaffidi, Xiangyu Cao. Does scrambling equal chaos? arXiv:1912.11063v1 [cond-mat.stat-mech] Dec 23, 2019.

https://arxiv.org/abs/1912.11063