Translate
martedì 1 luglio 2025
# game: Parrondo's paradox in space-inhomogeneous quantum walks.
sabato 15 marzo 2025
# qubit: communication power of a noisy qubit.
martedì 4 marzo 2025
# game: strategic decision making in biological and artificial brains.
giovedì 6 febbraio 2025
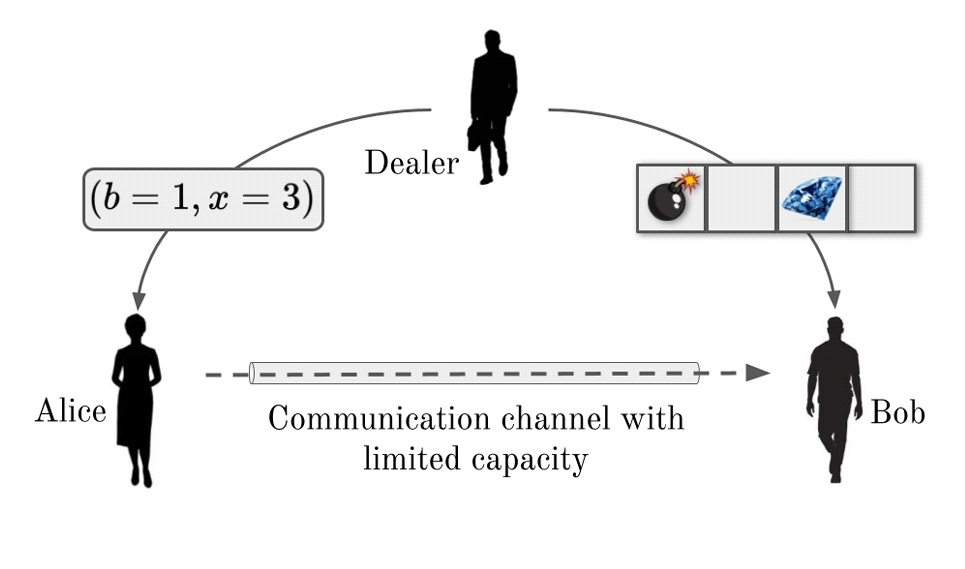
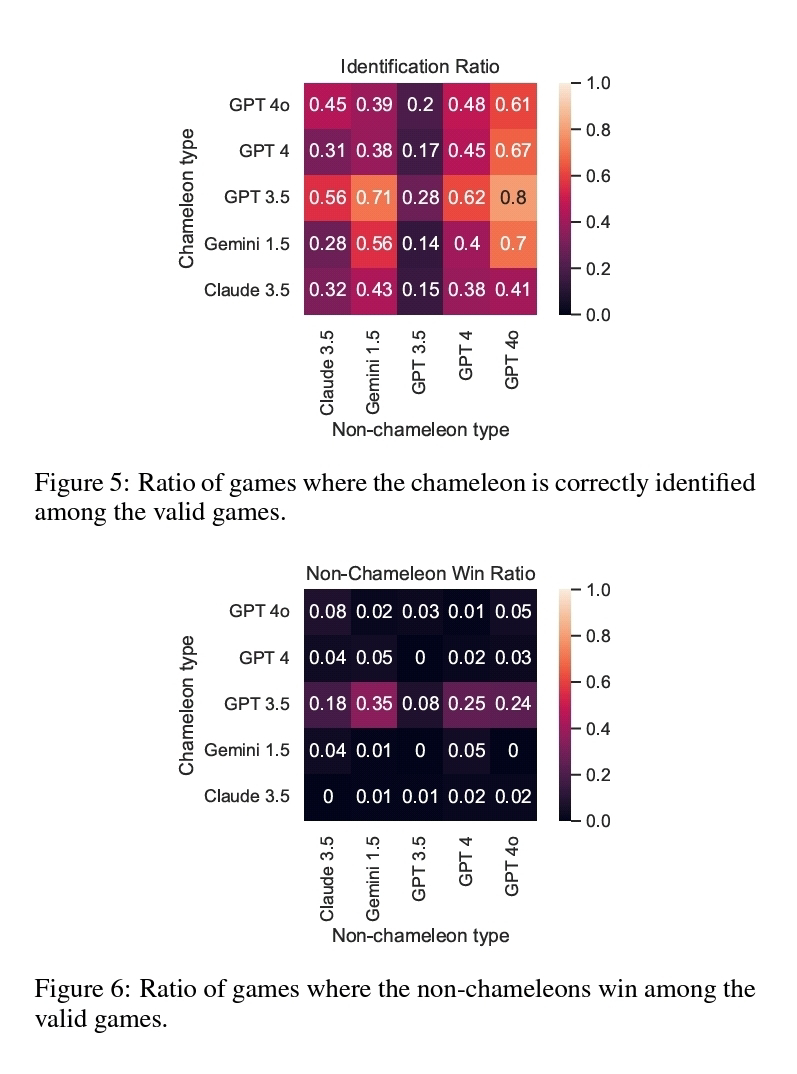
# life: chameleon machines
sabato 7 settembre 2024
# gst: phase transition of inertial self-propelled agents, a ‘inverse modeling’ approach.
martedì 17 ottobre 2023
# game: noise-induced Parrondo's paradox in discrete-time qu-walks
sabato 5 novembre 2022
# jazz: a 'Trombiverse' approach, 'hear Beethoven like you've never heard it before'
sabato 11 giugno 2022
# gst: switch to three players within the Parrondo game
sabato 19 febbraio 2022
# gst: Parrondo paradox revisited, a chaotic switching approach
mercoledì 14 agosto 2019
# game: inject irrationality into a game scenario; when a player will be their own worst enemy
<< in game theory, a game is defined as any type of scenario where there's an interaction between different decision-makers, or players, each of whom has well-defined preferences. >>
<< previous analyses assume the decision-makers always do what is best for them-they are fully rational-which is not always realistic. >>
<< So SFI Professor David Wolpert and economist Justin Grana, a former SFI postdoctoral scholar, wanted to inject some humanity into the players. They analyzed games with players who were subject to error, or "boundedly rational." >>
<< Our analysis shows that in many of these situations, a player will be their own worst enemy; >> David Wolpert.
Jenna Marshall. How much would you pay to change a game before playing it? Santa Fe Institute. Aug13, 2019. https://m.phys.org/news/2019-08-game.html
David Wolpert, Justin Grana. How Much Would You Pay to Change a Game before Playing It? Entropy 2019, 21, 686. doi: 10.3390/ e21070686. July 13, 2019. https://www.mdpi.com/1099-4300/21/7/686
mercoledì 7 agosto 2019
# game: 'pulsing' Parrondo to jump (and win) between two losing games
<< Parrondo’s paradox, in which losing strategies can be combined to produce winning outcomes, has received much attention in mathematics and the physical sciences; >>
<< In this review paper, the authors examine a large range of recent developments of Parrondo’s paradox in biology, across ecology and evolution, genetics, social and behavioral systems, cellular processes, and disease. >>
Kang Hao Cheong, Jin Ming Koh, Michael C. Jones. Paradoxical Survival: Examining the Parrondo Effect across Biology. BioEssays. Volume 41, Issue 6. doi: 10.1002/bies.201900027. May 27, 2019. https://onlinelibrary.wiley.com/doi/abs/10.1002/bies.201900027
Paradoxical Survival: Examining the Parrondo effect across biology. Singapore University of Technology and Design. Aug 5, 2019. https://www.sciencedaily.com/releases/2019/08/190805134043.htm
Also
"Parrondo" in: "Notes" & "FonT"