Translate
sabato 1 febbraio 2025
# gst: instability, shocks, and competition interfaces in the Brownian last-passage percolation model
lunedì 11 aprile 2022
# gst: apropos of instabilities, viscoelastic liquid bridges can be destabilized by torsion.
mercoledì 18 giugno 2025
# gst: spontaneous flow instability in active nematics; when quiescent and flowing states may coexist.
martedì 28 gennaio 2025
# gst: tuning to the edge of instability (in the cochlea)
venerdì 26 settembre 2025
# gst: instability and self-propulsion of flexible autophoretic filaments; it was observed distinct swimming modes, steadily translating "U" and metastable rotating "S" shapes.
lunedì 24 giugno 2024
# gst: buckling instability in a chain of sticky bubbles
lunedì 10 luglio 2023
# gst: myriad of complex dynamics from the atomization of acoustically levitated droplets
sabato 9 dicembre 2023
# gst: buckling instability of sticky bubbles.
giovedì 13 giugno 2024
# gst: helical instabilities from mixed mode transitions in boundary layers
giovedì 17 aprile 2025
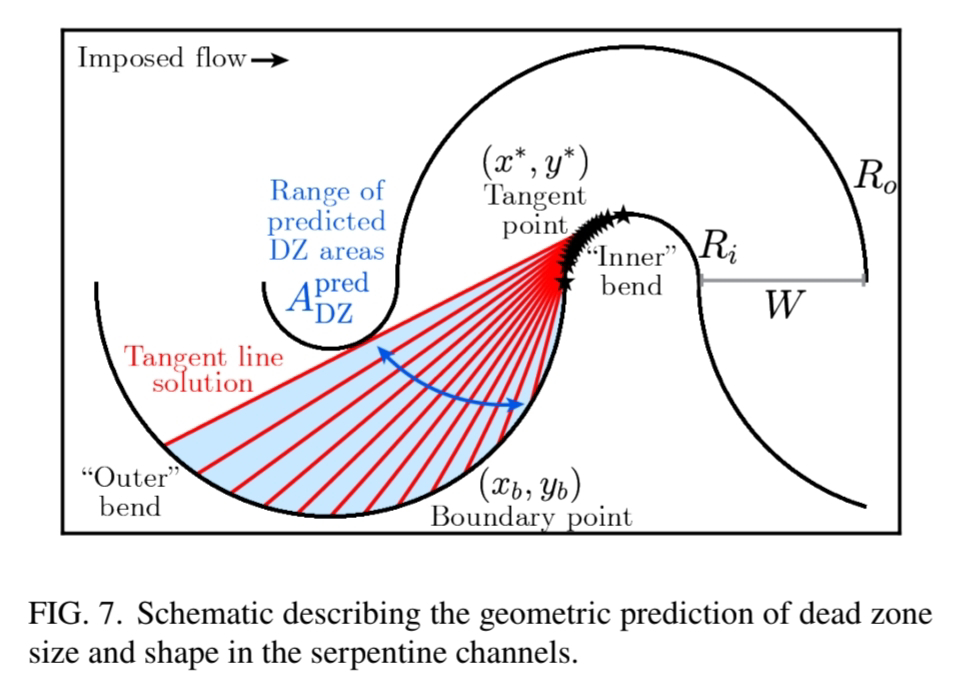
# gst: elastic instability of wormlike micelle solution flow in serpentine channels
martedì 26 settembre 2023
# gst: apropos of transitions, three distinct new families of long-wave instabilities and potential new pathways to turbulence.
lunedì 5 maggio 2025
# gst: transitions of breakup regimes for viscous droplets in airflow.
sabato 4 gennaio 2025
# gst: floating droplets excited with Faraday waves
sabato 3 dicembre 2016
# s-phys: how a plasmoid instability could behave
<< The paper describes how the plasmoid instability begins in a slow linear phase that goes through a period of quiescence before accelerating into an explosive phase that triggers a dramatic increase in the speed of magnetic reconnection. >>
<< Plasmoid instability, which breaks up plasma current sheets into small magnetic islands called plasmoids, has generated considerable interest in recent years as a possible mechanism for fast reconnection. >>
<< At issue is how magnetic reconnection, a universal process that sets off solar flares, northern lights and cosmic gamma-ray bursts, occurs so much faster than theory says should be possible. >>
John Greenwald. Researchers propose an explanation for the mysterious onset of a universal process. Nov. 22, 2016
http://m.phys.org/news/2016-11-explanation-mysterious-onset-universal.html
Comisso L., Lingam M., et al. General theory of the plasmoid instability. Phys. Plasmas 23, 100702 (2016);