# gst: biased random walks on networks with stochastic resetting.

<< This study explores biased random walk dynamics with stochastic resetting on general networks. (AA) show that the combination of biased random walks and stochastic resetting makes significant contributions by analyzing the search efficiency. (They) derive two analytical expressions for the stationary distribution and the mean first passage time, which are related to the spectral representation of the probability transition matrix of a biased random walk without resetting. These expressions can be used to determine the capacity of a random walker to reach the specific target and probe a finite network. >>

AA << apply the analytical results to two types of networks, pseudofractal scale-free webs and T-fractals, which are constructed through an iterative process. (They) also extend a strategy to explore other complex structure networks or larger networks by leveraging the spectral properties. >>

Anlin Li, Xiaohan Sun. Biased random walks on networks with stochastic resetting. Phys. Rev. E 111, 054309. May 16, 2025.

https://journals.aps.org/pre/abstract/10.1103/PhysRevE.111.054309

Also: walk, random, network, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, networks, randomness, random walk, stochasticity, stochastic resetting.

# gst: apropos of interweavings, linking dispersion and stirring in randomly braiding flows.

     Fig. 5 (a)

<< Many random flows, including 2D unsteady and stagnation-free 3D steady flows, exhibit non-trivial braiding of pathlines as they evolve in time or space. (AA) show that these random flows belong to a pathline braiding 'universality class' that quantitatively links dispersion and chaotic stirring, meaning that the Lyapunov exponent can be estimated from the purely advective transverse dispersivity. (AA) verify this quantitative link for both unsteady 2D and steady 3D random flows. This result uncovers a deep connection between transport and mixing over a broad class of random flows. >>️

Daniel R. Lester, Michael G. Trefry, Guy Metcalfe. Linking Dispersion and Stirring in Randomly Braiding Flows. arXiv: 2412.05407v1 [physics.flu-dyn]. Dec 6, 2024.

https://arxiv.org/abs/2412.05407

Also: random, chaos, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, random, random flows, randomly braiding flows, chaos

# gst: random trajectories in bounded domains

<< ️Can we deduce the total length of a random trajectory by observing only its local path segments within a confined domain? Surprisingly, the answer is yes—for curves randomly placed and oriented in space, whether stochastic or deterministic; generated by ballistic or diffusive dynamics; possibly interrupted by stopping or branching; and in two or more dimensions. More precisely, the mean total length ⟨𝐿⟩ relates to the mean in-domain path length ⟨ℓ⟩ and the mean chord length of the domain ⟨𝜎⟩ via the following simple and universal relation:

              1/⟨ℓ⟩ = 1/⟨𝐿⟩ + 1/⟨𝜎⟩

Here, ⟨𝜎⟩ is a purely geometric quantity, dependent only on the volume-to-surface ratio of the domain. Derived solely from the kinematic formula of integral geometry, the result is independent of step-length statistics, memory, absorption, and branching, making it equally relevant to photons in turbid tissue, active bacteria in microchannels, cosmic rays in molecular clouds, or neutron chains in nuclear reactors. Monte Carlo simulations spanning straight needles, Y shapes, and isotropic random walks in two and and three dimensions confirm the universality and demonstrate how a local measurement of ⟨ℓ⟩ yields ⟨𝐿⟩ without ever tracking the full trajectory. >>

T. Binzoni, E. Dumonteil, A. Mazzolo. Universal property of random trajectories in bounded domains. Phys. Rev. E 112, 044105. Oct 3, 2025.

https://journals.aps.org/pre/abstract/10.1103/dng6-9519

arXiv: 2011.06343v3 [math-ph]. May 16, 2025. 

https://arxiv.org/abs/2011.06343

Also: random, walk, walking, in https://www.inkgmr.net/kwrds.html 

Also: voli a casaccio (quasi-stochastic poetry). Oct 01, 2006.

https://inkpi.blogspot.com/2006/10/2066-voli-casaccio.html

Keywords: gst, randomness, random trajectories,  walk, random walk, bounded domains.

# gst: localization of active particles on random arrays of parallel filaments.

<< ️Quenched disorder in the environment can fundamentally alter transport dynamics in both active and passive systems. (AA) explore how disordered arrays of filaments govern the distribution of intermittently moving particles which switch between diffusive and processive transport. >>

<<️ Motivated by the mixed-polarity arrangements of parallel microtubules observed in mammalian dendrites, (They) show that such arrays tend to result in localization of particles at regions of convergent filament orientation. In the rapid attachment-detachment limit, the disordered system can be described by a noisy one-dimensional effective energy landscape, whose structure is approximated by a random walk. >>

<< ️The depth and width of wells on this landscape are expressed as a function of the transport kinetics and system geometry. Localization is shown to be strongest at intermediate run-lengths, where biased transport persists long enough to sense the quenched filament polarity but not so long as to facilitate escape from local traps. >>

<< ️These (AA) results demonstrate robust localization of particles moving on random filament networks, highlighting the emergent spatial organization that arises from an interplay of active transport and quenched disorder. >>

Owen Santoso, Elena Koslover. Localization of Active Particles on Random Arrays of Parallel Filaments. arXiv: 2606.00286v1 [cond-mat.dis-nn]. May 29, 2026.

https://arxiv.org/abs/2606.00286

Also: noise, disorder, disorder & fluctuations, random, intermittency, escape, particle, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, noise, disorder, disorder & fluctuations, randomness, intermittency, escape, particles, quenched disorder, transport dynamics, diffusive and processive transport, arrays of filaments, random walk, random filament networks, escape from local traps.

# behav: souvenir collector's walk; the distribution of the number of steps of a continuous-time random walk ending at a given position.

AA << consider a random walker performing a continuous-time random walk (CTRW) with a symmetric step lengths' distribution possessing a finite second moment and with a power-law waiting time distribution with finite or diverging first moment. The problem (They) pose concerns the distribution of the number of steps of the corresponding CTRW conditioned on the final position of the walker at some long time 𝑡. >>

<< ️For positions within the scaling domain of the probability density function (PDF) of final displacements, the distributions of the number of steps show a considerable amount of universality, and are different in the cases when the corresponding CTRW corresponds to subdiffusion and to normal diffusion. >>

They << ️moreover note that the mean value of the number of steps can be obtained independently and follows from the solution of the Poisson equation whose right-hand side depends on the PDF of displacements only. >>

<< ️This approach works not only in the scaling domain but also in the large deviation domain of the corresponding PDF, where the behavior of the mean number of steps is very sensitive to the details of the waiting time distribution beyond its power-law asymptotics. >>

Igor M. Sokolov. Souvenir collector's walk: The distribution of the number of steps of a continuous-time random walk ending at a given position. Phys. Rev. E 112, 024101. Aug 1, 2025

https://journals.aps.org/pre/abstract/10.1103/6j5n-bqcf

Also: behav, walk, walking, random, in https://www.inkgmr.net/kwrds.html 

Keywords: behavior, walk, walking, random walks, randomness.

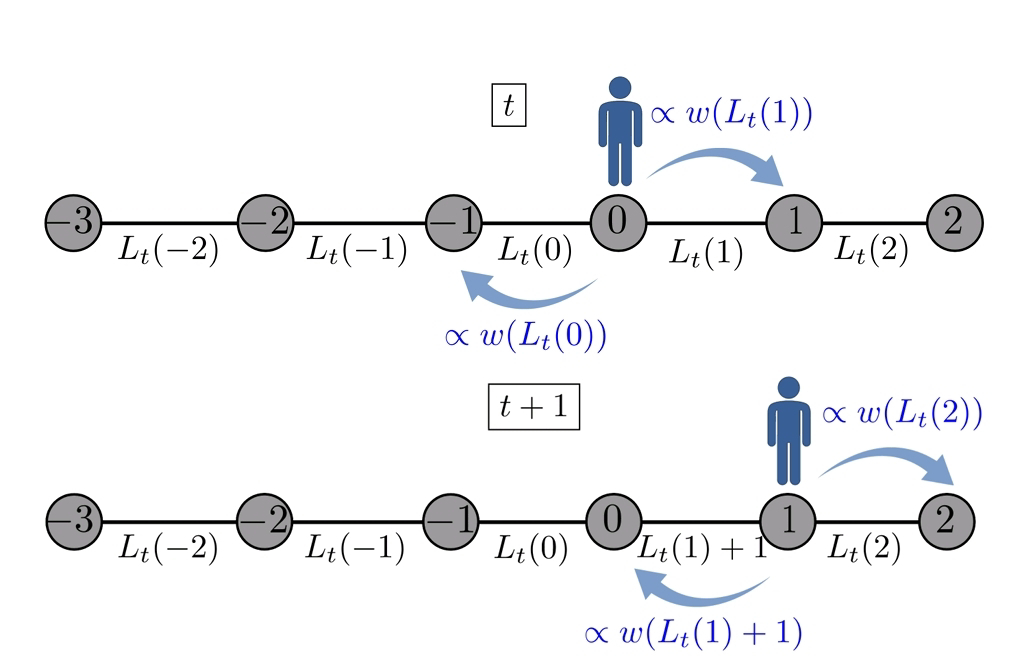
# gst: apropos of random walks, intermittent random walks under stochastic resetting

AA << analyze a one-dimensional intermittent random walk on an unbounded domain in the presence of stochastic resetting. In this process, the walker alternates between local intensive search, diffusion, and rapid ballistic relocations in which it does not react to the target. >>

AA << demonstrate that Poissonian resetting leads to the existence of a non-equilibrium steady state. (They) calculate the distribution of the first arrival time to a target along with its mean and show the existence of an optimal reset rate. In particular, (..) the initial condition of the walker, i.e., either starting diffusely or relocating, can significantly affect the long-time properties of the search process. >>

<< the presence of distinct parameter regimes for the global optimization of the mean first arrival time when ballistic and diffusive movements are in direct competition. >>️

Rosa Flaquer-Galmes, Daniel Campos,  Vicenc Mendez. Intermittent random walks under stochastic resetting. Phys. Rev. E 109, 034103. March 4, 2024. 

https://journals.aps.org/pre/abstract/10.1103/PhysRevE.109.034103  

Also: walk, walking, random, in https://www.inkgmr.net/kwrds.html

Keywords: gst, walk, intermittent random walk, stochasticity, stochastic resetting

# behav: decomposition of anomalous diffusion in two-state random walks.

<< ️Two-state stochastic models, where motion alternates between distinct dynamical modes, are widely observed in complex systems. Here (AA) study the Two-State Random Walk (TSRW), which switches between a continuous-time random walk (CTRW) rest state and a standard Lévy walk (LW) motion state, each with power-law distributed sojourn times. >>

<< ️Using anomalous diffusion decomposition, (They) show that TSRWs exhibit a generic coexistence of Joseph (correlation), Noah (heavy-tailed increments), and Moses (aging) effects. >>

<< ️Strikingly, although classical Lévy walks alone possess only the Joseph effect, both Noah and Moses effects emerge in TSRWs solely due to stochastic switching with the CTRW phase. >>

<< ️(Their) results demonstrate that coupling between dynamical states can fundamentally reshape the mechanisms driving anomalous diffusion, offering a minimal yet powerful framework for transport in heterogeneous and intermittently switching environments. >>

Abhijit Bera, Kevin. E. Bassler. Decomposition of Anomalous Diffusion in two-state random walks. arXiv: 2606.00149v2 [nlin.AO]. Jun 7, 2026.

https://arxiv.org/abs/2606.00149

Also: behav, random, walk, walking, in https://www.inkgmr.net/kwrds.html 

Keywords: behavior, randomness, walk, walking, two-state stochastic behavior, two-state random walk, stochastic switching, Lévy walk motion, Joseph Noah Moses effects, anomalous diffusion, heterogeneous and intermittently switching environments. 

# gst: quantum walk on a random comb.

<< ️(AA) study continuous time quantum walk on a random comb graph with infinite teeth. Due to localization effects along the spine, the walk cannot go to infinity in the spine direction, while it can escape to infinity along the teeth of the comb. Starting from an initial vertex the walk has a nonzero probability to stay trapped in a finite region. These results are obtained by studying the spectrum and eigenstates of the random Hamiltonian for the graph and analysing its properties. (They) use both analytic and numerical methods many of which come from the theory of Anderson localization in one dimension. >>

François David, Thordur Jonsson. Quantum walk on a random comb. arXiv: 2604.00908v1 [quant-ph]. Apr 1, 2026.

https://arxiv.org/abs/2604.00908

Also: Francois David, Thordur Jonsson (2021). Quantum walk on a comb with infinite teeth. 

https://arxiv.org/abs/2107.08866    Bergfinnur Durhuus, Thordur Jonsson, John Wheater (2005). Random walks on combs. 

https://arxiv.org/abs/hep-th/0509191

Also: walk, random, escape, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, combs, walk, quantum walk, escape, randomness.

# evol: the hypothesis of quasi-stochastic 'jazzy' metamechanics of biological evolution (in Arabidopsis thaliana)

<< Mutations occur when DNA is damaged and left unrepaired, creating a new variation. The scientists wanted to know if mutation was purely random or something deeper. What they found was unexpected. >>️

<< We always thought of mutation as basically random across the genome, (..) It turns out that mutation is very non-random and it's non-random in a way that benefits the plant. It's a totally new way of thinking about mutation. >> Grey Monroe. ️

Study challenges evolutionary theory that DNA mutations are random. UC Davis. Jan 12, 2022.

https://phys.org/news/2022-01-evolutionary-theory-dna-mutations-random.html

Monroe JG, Srikant T, et al. Mutation bias reflects natural selection in Arabidopsis thaliana. Nature. doi: 10.1038/ s41586-021-04269-6. Jan 12, 2022.

https://www.nature.com/articles/s41586-021-04269-6

FonT 

for a long time I have developed the suspicion that the small plant cared for by grandmother on the windowsill could be a not trivial image of (r)evolution ... 

The three ways of the plastoquinone inside the photosystem II complex. May 23, 2017.

https://flashontrack.blogspot.com/2017/05/s-phyto-three-ways-of-plastoquinone.html

Also

keyword 'evolution'  in FonT

https://flashontrack.blogspot.com/search?q=evolution

keyword 'evolution' | 'evoluzione'  in Notes (quasi-stochastic poetry)

https://inkpi.blogspot.com/search?q=evolution

https://inkpi.blogspot.com/search?q=evoluzione

keyword 'jazz' in FonT

https://flashontrack.blogspot.com/search?q=jazz

keyword 'jazz' in Notes (quasi-stochastic poetry):

https://inkpi.blogspot.com/search?q=jazz

keywords: evol, dna, mutations, randomness, quasi-stochasticity, jazz

# gst: randomness with constraints: constructing minimal models for high-dimensional biology.

<< ️Biologists and physicists have a rich tradition of modeling living systems with simple models composed of a few interacting components. Despite the remarkable success of this approach, it remains unclear how to use such finely tuned models to study complex biological systems composed of numerous heterogeneous, interacting components. >>

<< ️One possible strategy for taming this biological complexity is to embrace the idea that many biological behaviors we observe are ``typical'' and can be modeled using random systems that respect biologically-motivated constraints. Here, (AA) review recent works showing how this approach can be used to make close connection with experiments in biological systems ranging from neuroscience to ecology and evolution and beyond. Collectively, these works suggest that the ``random-with-constraints'' paradigm represents a promising new modeling strategy for capturing experimentally observed dynamical and statistical features in high-dimensional biological data and provides a powerful minimal modeling philosophy for biology. >>

Ilya Nemenman, Pankaj Mehta. Randomness with constraints: constructing minimal models for high-dimensional biology. arXiv: 2509.03765v1 [physics.bio-ph]. Sep 3, 2025.

https://arxiv.org/abs/2509.03765

Also: random, transition, disorder & fluctuations, fly at random, quasi-stochastic poetry, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, randomness, transitions, disorder & fluctuations, random-with-constraints, fly at random, quasi-stochastic poetry.

# gst: random walk model for dual cascades in wave turbulence.

<< Dual cascades in turbulent systems with two conserved quadratic quantities famously arise in both two-dimensional hydrodynamic turbulence and also in wave turbulence based on four-wave interactions. >>

<< in wave turbulence the systematic spectral fluxes observed in a dual cascade do not require an irreversible dynamical mechanism, rather, they arise as the inevitable outcome of blind chance. >>️️

Oliver Bühler. Random walk model for dual cascades in wave turbulence. Phys. Rev. E 109, 055102. May 1, 2024. 

https://journals.aps.org/pre/abstract/10.1103/PhysRevE.109.055102

Also: waves, turbulence, random, weak, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, waves, turbulence, weak turbulence, random, random walks

# gst: apropos of absorbing targets, persistence exponents of self-interacting random walks

<< The persistence exponent, which characterizes the long-time decay of the survival probability of stochastic processes in the presence of an absorbing target, plays a key role in quantifying the dynamics of fluctuating systems. Determining this exponent for non-Markovian processes is known to be a difficult task, and exact results remain scarce despite sustained efforts. >> 

In their Letter, AA << consider the fundamental class of self-interacting random walks (SIRWs), which display long-range memory effects that result from the interaction of the random walker at time 𝑡 with the territory already visited at earlier times 𝑡′ <𝑡. (AA)  compute exactly the persistence exponent for all physically relevant SIRWs. As a byproduct, (They) also determine the splitting probability of these processes. >>

<< Besides their intrinsic theoretical interest, these results provide a quantitative characterization of the exploration process of SIRWs, which are involved in fields as diverse as foraging theory, cell biology, and nonreversible Monte Carlo methods. >>

J. Brémont, L. Régnier, et al. Persistence Exponents of Self-Interacting Random Walks. Phys. Rev. Lett. 134, 197103. May 16, 2025.

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.134.197103

arXiv:2410.18699v1 [cond-mat.stat-mech]. 

https://arxiv.org/abs/2410.18699

Also: walk, walking, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, walk, walking, self-interacting random walk, walker self-repulsion, walker self-attraction, stochasticity, absorbing targets.

# gst: apropos of ambiguous scenarios, very persistent random walkers reveal transitions in landscape topology

AA << study the typical behavior of random walkers on the microcanonical configuration space of mean-field disordered systems. Passive walks have an ergodicity-breaking transition at precisely the energy density associated with the dynamical glass transition, but persistent walks remain ergodic at lower energies. >>

<< In models where the energy landscape is thoroughly understood, (They) show that, in the limit of infinite persistence time, the ergodicity-breaking transition coincides with a transition in the topology of microcanonical configuration space. (They) conjecture that this correspondence generalizes to other models, and use it to determine the topological transition energy in situations where the landscape properties are ambiguous. >>

Jaron Kent-Dobias. Very persistent random walkers reveal transitions in landscape topology. arXiv: 2505.16653v2 [cond-mat.dis-nn]. May 23, 2025. 

https://arxiv.org/abs/2505.16653

Also: random, walk, walking, disorder, transition, in https://www.inkgmr.net/kwrds.html

Also: ambiguity in FonT  https://flashontrack.blogspot.com/search?q=ambiguity     ambiguity in Notes (quasi-stochastic poetry)  https://inkpi.blogspot.com/search?q=ambiguita

Keywords: mean-field disordered systems, disorder, randomness, random walker, transitions, topological transition energy, ambiguity.

# gst: apropos of weakly coupled oscillators, a new approach to depict about their spontaneous stochastic activities

<<  Many systems in physics, chemistry and biology exhibit oscillations with a pronounced random component. Such stochastic oscillations can emerge via different mechanisms, for example linear dynamics of a stable focus with fluctuations, limit-cycle systems perturbed by noise, or excitable systems in which random inputs lead to a train of pulses. Despite their diverse origins, the phenomenology of random oscillations can be strikingly similar. >>

<< Here (AA) introduce a nonlinear transformation of stochastic oscillators to a new complex-valued function Q∗1(x) that greatly simplifies and unifies the mathematical description of the oscillator's spontaneous activity, its response to an external time-dependent perturbation, and the correlation statistics of different oscillators that are weakly coupled. >>

AA << approach makes qualitatively different stochastic oscillators comparable, provides simple characteristics for the coherence of the random oscillation, and gives a framework for the description of weakly coupled oscillators. >>️

Alberto Pérez-Cervera, Boris Gutkin, et al. A Universal Description of Stochastic Oscillators. arXiv: 2303.03198v1 [nlin.AO]. Feb 27, 2023. 

https://arxiv.org/abs/2303.03198

Also

'oscillations' in FonT

https://flashontrack.blogspot.com/search?q=oscillations

Keywords: gst, oscillations, random oscillations, weakly coupled oscillators

# gst: apropos of control by noise, diffusive transport from spatially correlated random phase kicks.

<< ️(AA) study the dynamics of a single-particle wave packet on a one-dimensional lattice subject to periodic random phase kicks with finite spatial correlation length. This stroboscopic setting provides a controllable model of dephasing in driven quantum systems. >>

<< ️Using a momentum-space formulation, (They) show that the evolution is governed by an accumulated phase whose structure determines the spreading of the wave packet. (They) find that the phase kicks strongly suppress ballistic transport and induce diffusion at long times. (They) derive an explicit analytical expression for the diffusion coefficient as a function of the correlation length, in excellent agreement with numerical simulations. >>

<< (Their) results uncover a simple mechanism by which spatially correlated phase noise controls quantum transport, and provide a quantitatively testable prediction for diffusion in periodically driven lattice systems. Possible experimental realizations in cold-atom platforms are discussed. >>

Pei Wang. Diffusive transport from spatially correlated random phase kicks. arXiv: 2605.06701v1 [cond-mat.mes-hall]. May 5, 2026.

https://arxiv.org/abs/2605.06701

Also: particle, waves, random, noise, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, particle, waves, randomness, noise, single-particle wave packet, periodic random phase kicks, spatially correlated phase noise, quantum transport.

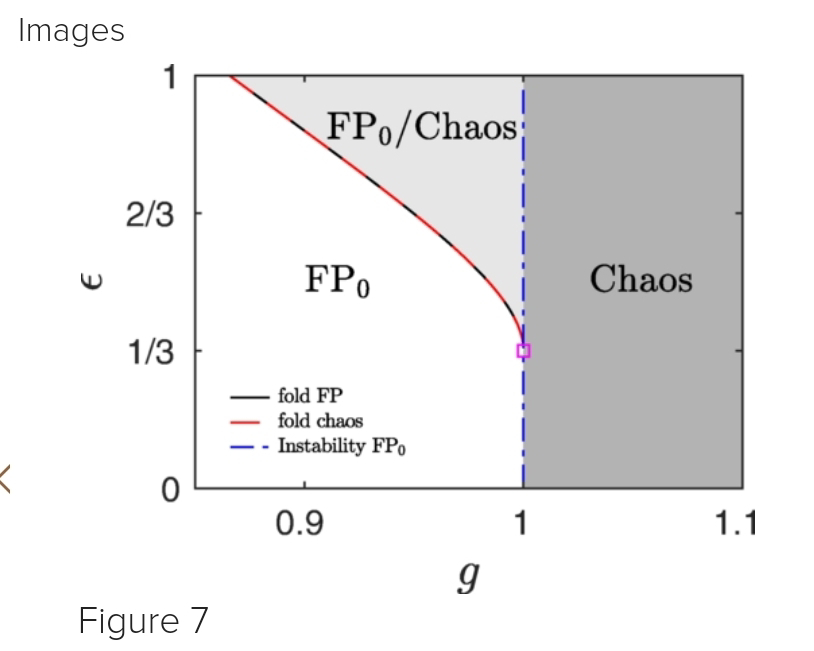
# gst: discontinuous transition to chaos in a canonical random neural network

AA << study a paradigmatic random recurrent neural network introduced by Sompolinsky, Crisanti, and Sommers (SCS). In the infinite size limit, this system exhibits a direct transition from a homogeneous rest state to chaotic behavior, with the Lyapunov exponent gradually increasing from zero. (AA)  generalize the SCS model considering odd saturating nonlinear transfer functions, beyond the usual choice 𝜙⁡(𝑥)=tanh⁡𝑥. A discontinuous transition to chaos occurs whenever the slope of 𝜙 at 0 is a local minimum [i.e., for 𝜙′′′⁢(0)>0]. Chaos appears out of the blue, by an attractor-repeller fold. Accordingly, the Lyapunov exponent stays away from zero at the birth of chaos. >>

In the figure 7 << the pink square is located at the doubly degenerate point (𝑔,𝜀)=(1,1/3). >>️️

Diego Pazó. Discontinuous transition to chaos in a canonical random neural network. Phys. Rev. E 110, 014201. July 1, 2024.

https://journals.aps.org/pre/abstract/10.1103/PhysRevE.110.014201

Also: chaos, random, network, transition, neuro, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, chaos, random, network, transition, neuro

# gst: apropos of transitions, randomness can stabilize edge states in short- lifetime regions of disordered periodically-driven systems

<< lifetimes of the edge states exhibit universal behavior when random potentials exist since the edge- and bulk- dominant eigenstates are mixed, leading to that lifetimes are prolonged by random potentials in the region II (short- lifetime region) and shortened in the region I (long- lifetime region). >>

<<  it is an intriguing phenomenon that random potentials tend to stabilize edge states in the region II (short- lifetime regions). >>

Ken Mochizuki, Kaoru Mizuta, Norio Kawakami. Fate of Topological Edge States in Disordered Periodically-driven Nonlinear Systems. arXiv: 2108.00649 (nlin). Aug 2, 2021.

https://arxiv.org/abs/2108.00649

Also

keyword 'random' in FonT

https://flashontrack.blogspot.com/search?q=random

keyword 'disorder' in FonT

https://flashontrack.blogspot.com/search?q=disorder

keyword 'disordine' in Notes (quasi-stochastic poetry)

https://inkpi.blogspot.com/search?q=disordine

# gst: random interaction in active matter models; critical changes in Vicsek's scenario.

<< Randomness plays a key role in the order transition of active matter but has not yet been explicitly considered in pairwise interaction connection. In this paper, (AA) introduce the perception rate 𝑃 into the Vicsek model as the probability of the interaction connections and model the connections as superposition states. (They) show that with increasing 𝑃, the polar order number undergoes an order transition and then saturation. >>

<< The order transition is a first-order phase transition with band formation, and the effect of 𝑃 is different from density. The change of the order number is linked with the interaction structure. The order transition, order saturation, and phase separation correspond to different critical changes in the local interaction number. >>

<< The global interaction structure is further analyzed as a network. The decrease of 𝑃 is comparable to random edge removal, under which the network experiences modal transitions near the critical points of the order number, and the network exhibits surprising robustness.  (AA) results suggest that random interaction can be a new important factor in active matter models, with potential applications in robotic swarms and social activities. >>

Ruizhi Jin, Kejun Dong. Role of random interaction connection in the order transition of active matter based on the Vicsek model. Phys. Rev. E 111, 064122. Jun 17, 2025.

https://journals.aps.org/pre/abstract/10.1103/9rdd-tbn7

arXiv: 2501.10669v1 [cond-mat.soft]. Jan 18, 2025. 

https://arxiv.org/abs/2501.10669

Also: network, random, perception, transition, swarm, in https://www.inkgmr.net/kwrds.html 

Keywords: gst, active matter, network, randomness, perception, criticality, transitions, swarm.

# gst: random walk to describe a interplay between the inter-chain hopping and the intra-chain hopping in amorphous Polyimide nanofibers

AA << report the observation of a crossover of heat conduction behavior from three dimensions (3D) to quasi-one dimension (1D) in Polyimide(PI) nanofibers at a given temperature. A theoretical model based on the random walk theory has been proposed to quantitatively describe the interplay between the inter-chain hopping and the intra-chain hopping in nanofibers. This model explains well the diameter dependence of thermal conductivity and also speculates the upper limit of thermal conductivity of amorphous polymers in the quasi-1D limit. >>

Lan Dong, Qing Xi, et al. Dimensional crossover of heat conduction in amorphous Polyimide nanofibers. National Science Review. nwy004.  doi: 10.1093/nsr/nwy004. Jan 09,  2018.

https://academic.oup.com/nsr/advance-article/doi/10.1093/nsr/nwy004/4794956

<< The intrinsic structure of amorphous polymers is highly disordered with long, entangled molecular chains >>

Science China Press. "Random walk" of heat carriers in amorphous polymers. Mar 01, 2018.

https://m.phys.org/news/2018-03-random-carriers-amorphous-polymers.html

gst: actually and counterintuitively a coherent jump could generate disorder.

AA << consider a quantized version of a model for “random walk in random environment.” (..) For a ring geometry (a chain with periodic boundary condition) it features a delocalization-transition as the bias in increased beyond a critical value, indicating that the relaxation becomes underdamped. Counterintuitively, the effective disorder is enhanced due to coherent hopping. >>

Ben Avnit, Doron Cohen. Quantum walk in stochastic environment. Phys. Rev. E 108, 054111. Nov 7, 2023. 

https://journals.aps.org/pre/abstract/10.1103/PhysRevE.108.054111

Also:  Voli a casaccio. Notes (quasi-stochastic poetry). Oct 01, 2006.

https://inkpi.blogspot.com/2006/10/2066-voli-casaccio.html

Also: 'random', 'transition', 'disorder', 'chaos', in https://www.inkgmr.net/kwrds.html

Keywords: gst, walk, random walk, quantum walk, qu-walk, jump, transition, disorder, chaos